推定方法における最小二乗法

（平成23年9月19日現在）

９－１．最小二乗法の計算原理

　今までに見てきたように、母数の推定・検定もしくは、その期待値を求めるために、線形モデルで考える理論を線形推測論といいます。

　線形モデルには様々なモデルが考案されていますが、最もポピュラーに利用されているモデルが最小二乗法です。１元１次回帰分析における最小二乗法については、すでに２－３で解説していますが、ここで一般論に発展させた最小二乗法について解説していきます。

　各データ結果ベクトルをｙ、未知の母数ベクトルをθ、誤差ベクトルεとすれば、ベクトル列は次のように表現できます。

　，，

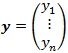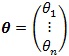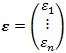
　そして、係数行列Xとすれば、線形モデルは次のように表現できます。係数行列Xは既知の数値であり、すでに与えられているものです。

　さて、線形モデルでは、未知母数θに係数列ベクトルLによる線形結合による線形推定量（次式L'θ）の最良線形不偏推定量（best linear unbiased estimator）を求めることです。

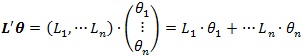
【注意】’（プライム）は転置の記号。転置記号があると、列ベクトルは行ベクトル、行ベクトルは列ベクトルへ転置される。転置記号には、プライムの代わりに「T」を記号したり、左上に小文字の「ｔ」を記号したりするケースもある。

　誤差εの性質として次の性質を仮定するならば、最良線形不偏推定量は与えられた係数LにおけるL’θの分散を最小化させるθを求めているに他なりません。

[誤差εの条件]

(1)不偏性；　E(ε）＝０　　

(2)等分散性とi≠ｊにおける誤差項の無相関性；　 　　行列Iは単位行列

　ただ、L'θの分散最小化は、ベクトルLが具体的に与えられるたびに計算しなければならないので非常に煩雑となります。そこで利用されるのが最小二乗法です。最小二乗法は、ガウスとマルコフによって証明された定理を利用したもので、観測値ｙと期待値Xθの偏差二乗和を最小化させるθはL'θの最良線形不偏推定量とθになるというものです。これにより、列ベクトルLに依存することなく、容易にL'θの最良線形不偏推定量を求めることができるのです。

　偏差二乗和を行列で表すと次のようになります。

　これを最小化するθは、偏差二乗和をθで偏微分しゼロとなるθとなります。計算すると以下のようになります。

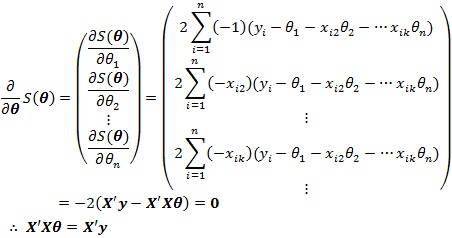
　上記のとおり、最後の式を正規方程式（normal equation）といいます。この方程式の解であるθが最良線形不偏推定量となります。この方程式は逆行列を用いた行列計算によって求めることができます。

９－２．ガウス・マルコフの定理

　ガウス・マルコフの定理をここで詳しく解説します。

　ガウス・マルコフの定理（Gauss-Markov's theorem）とは、最小二乗法によって求められたθが線形モデルにおける不偏で、かつ、分散が最小となる推定量であるという定理をいいます。この定理があるからこそ、不偏推定量を求める方法として、最小二乗法を採用することが認められるし、また、一般的に最小二乗法による回帰分析が多用されることになるのです。

【定理】ガウス・マルコフの定理

以下の仮定（ガウス・マルコフの仮定）が存在する場合、最小二乗法によって求められた推定量は最良線形不偏推定量となる。

[条件]

(1)不偏性；　E(ε）＝０　　

(2)等分散性とi≠ｊにおける誤差項の無相関性；　 　　行列Iは単位行列

【証明】

　まず、不偏推定量となることを証明します。正規方程式をθについて解くと以下のとおりとなります。

　任意のL'θについて次のようにおきます。

　上記の期待値を計算すると、次のようになります。

　上記のとおり、正規方程式の解であるθハット（ハットは記号の上の「^」の記号）による任意の線形結合L'θハットの期待値はL'θの不偏推定量となることがわかります。

　次に、最小分散となることを証明します。任意の線形不偏推定量をT'yとすると、L'θハットとT'yの差額の期待値は次のようになります。

　なお、E(T'y）は不偏推定量であるため、L'θとなることは明らかです。さて、上記の式がなりたつためには、次の等式が成り立つ必要があります。

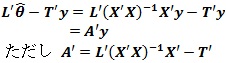
　さて、分散式を以下のように計算する次のようになります。

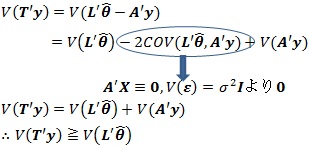
　上記のように、任意の線形不偏推定量T'yよりもL'θハットの分散が小さくなることから最も分散の小さい線形不偏推定量となります。[証明終了]。

[追補]

逆行列が存在しない（一意的な解が存在しない）場合には、上記の計算が実施できません。この場合、様々な方法が考えられますが、線形代数の一般化逆行列の理論を利用して証明することができます。線形代数の一般化逆行列は数学的に難易度が高いことから、このシリーズでは解説しません。