現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。
(平成23年7月1日現在)
8-1.推定の意義
確率統計学の重要な分野が推定理論です。推定理論は、標本抽出されたものから算出された標本平均や標本分散から母集団の確率分布の平均や分散(すなわち母数)を推定していくこと理論です。
例えば、交通事故がポアソン分布に従うとわかっていても、ポアソン分布の母数であるλがどのような値であるかがわからなければ、「どのような」ポアソン分布に従っているのか把握することができません。交通事故の確率分布を把握できなければ正しい道路行政を行うこともできず、適切な予算配分を達成することもできません。
結局、確率統計学が実世界で有意義な学問であるためには、母数を確定できる確立された理論が必要であると言えます。母数を確定させる理論は、前述したように、全調査することが合理的ではない(もしくは不可能である)母集団の母数を確定するために標本によって算定された標本平均や標本分散などを母集団の母数へ昇華させることに他なりません。
母数の推定の方法には、点推定(point estimation)と区間推定(interval estimation)があります。点推定は1つの値に推定する方法であり、区間推定は真のパラメータの値が入る確率が一定以上と保証されるような区間で求める方法です。
8-2.モーメント法による点推定
点推定のオーソドックスな方法として、モーメント法(method of moments)があります。モーメント法は多元連立方程式を解くことで母数を求める方法です。
母集団が、k個の母数をもつ確率分布に従うと仮定します。それぞれの母数はθ1、θ2、θ3・・・θkとすると、この母集団のモーメントは、モーメント母関数gにより次のように表現することができます(例えば、k次モーメント)。
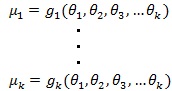
上記の関数は1次モーメントからk次モーメントまでk個の関数で表現されます。
一方、モーメントはその定義から、![]() であり、標本モーメントは定義から次ののように表現できます。
であり、標本モーメントは定義から次ののように表現できます。
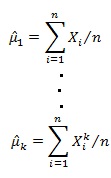
このことから、標本モーメントで各モーメントが計算され、それを関数gに順次当てはめていくことで母集団の各モーメントが算定され、母集団のパラメータを求めることができます。
8-3.最尤法による点推定
最尤法(maximum likelihood method)も点推定の方法として代表的なものです。最尤法は、「さいゆうほう」と読みます。最尤法は、尤度関数(likelihood function)とよばれる関数を設定し、その関数の最大化する推定値をもって母数を決定する方法です。
最尤法は、ある標本結果が与えられたものとして、その標本結果が発生したのは確率最大のものが発生したとして確率分布を考える方法です。
例えば、1が出る確率p、0が出る確率が1-pのある二項分布を想定します。二項分布の母数はpであり、このpを求めれば、「ある二項分布」はどういう二項分布かを決定することができます。
この実験を10回実施したところ、(1,1,1,0,1,0,1,0,0,1)という結果になったとします。この10回の結果はつまり「標本」であり、どんな二項分布であっても発生する可能性があるものです。極端に確率pが0.0001%であってもこういった標本結果となる可能性はゼロではありません。
しかし、確率pが0.0001%だったとしたら、この標本結果をみて「こんなに1が出ることはないだろう」と誰もが思うと思います。すなわち、「1が10回中6回出たのであれば、1の出る確率はもっと高いはず」と考えるのです。
このことは、逆説的に、「10回中6回も1が出たのであれば確率は6/10、すなわち『60%』だ」と言われたとしたら、どうでしょうか。「事実として、10回中6回が1だったのだから、そうだろう」というのが一般的な反応ではないかと思います。これがまさに、最尤法なのです。つまり、標本結果が与えたその事実から、母集団の確率分布の母数はその標本結果を提供し得るもっともらしい母数であると推定する方法なのです。
一般的に、標本の大きさがnのとき、尤度関数は、母数θとすると、次のように表現することができます。
![]()
これは確率変数Xの同時確率分布をθの関数とし、f(x,θ)とした場合に、尤度関数を確率関数の積として表現できるものです。また、母数が複数個ある場合には、次のように表現できます。
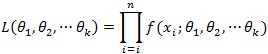
なお、尤度関数は上記のように確率関数の積として表現されるため、対数をとって、対数尤度関数として和に変換して取り扱うことがよくあります。
8-4.区間推定の方法
点推定が1つの母数を求めることであるのに対し、区間推定は母数θがある区間に入る確率が一定以上になるように保証する方法です。これを数式で表すと次のようになります。
![]()
つまり、上記のLとUの確率変数を求めることが区間推定になります。なお、Lを下側信頼限界(lower confidence limit)、Uを上側信頼限界(upper confidence limit)、区間[L,U]は1ーα%信頼区間(confidence interval)、1-αを信頼係数(confidence coefficient)といいます。なお、1-αは場合によって異なりますが、「90%信頼区間」、「95%信頼区間」、「99%信頼区間」がよく用いられている信頼区間になります。例えば、銀行のバリュー・アット・リスクでは99%信頼区間が用いられています。
例えば、正規母集団の母平均、母分散の区間推定を考えてみましょう。標本平均![]() は、正規分布
は、正規分布![]() に従うため、これを標準化して表現すると次のようになります。
に従うため、これを標準化して表現すると次のようになります。
![]()
これを展開すると、
![]()
よって信頼区間は、次のように表現できます。
![]()
なお、σが未知数のときは、標本分散の不偏分散sを代入して求めることもできます(自由度kのスチューデントのt分布)。
次に標本分散sを用いて、母分散σの信頼区間を表現すると次のようになります。
![]()
これは、標本分散sと母分散σの上記の関係が自由度n-1の![]() 分布に従うためです。
分布に従うためです。
よって、信頼区間は次のように計算できます。
![]()
8-5.仮説検定
統計的な論理として、仮説検定(hypothesis testing)というものがあります。仮説検定は、その名のとおり、「仮説をたてて、その仮説が正しいかどうかを検定する」ことですが、「正しいかどうか検定する方法」に確率論が利用されていることから、確率統計学の一分野として学習されるものになっています。
ここで、仮説検定では、その仮説が「正しい」かどうかを有意(significant)と表現しています。また、「正しくない」場合は「棄却」(reject)、「正しい場合」は「採択」(accept)といいます。検定結果としての「棄却」「採択」はあくまで設定した確率水準(それを
有意水準(significance level)といいます。)に基づいて行われるものです。例えば、「弁護士の平均年収は1,500万円以上だ」という仮説をたて、その有意水準が1%だったとしたら、平均1,500万円以上となった確率が5%だったとすると、「まぁ、あってもおかしくないよね」ということで、その仮説は「採択」ということになります。別の言い方をすれば「棄却されなかった」ということになるのです。
しかし、仮説検定で注意しなければならないのは、「棄却されなかった」からといって積極的に肯定しているわけではないということです。あくまでも「設定した有意水準では棄却されなかった」というだけで、例えば有意水準が10%であれば、5%というのは稀な出来事になるため「棄却」されてしまいます。逆説的にはなりますが、「棄却された」からといって、その反対を積極的に肯定しているわけでもないということでもあります。
仮説検定は、先の「弁護士の平均年収1,500万円以上」という仮説を帰無仮説(null hypothesis)とすると、「弁護士の平均年収は1,500万円以下」という仮説を対立仮説(alternative hypothesis)といいます。
仮説検定は、あくまで統計・確率的な観点からの検定であるため、真実と異なる結果を導いてしまう可能性があります。先の弁護士の平均年収のテーマであれば、真実は1,500万円以上の平均年収であるものを、「1,500万円以上ではない。つまり、棄却する」という結論を出してしまう検定の誤りが発生する可能性があるということです。これを「第一種の誤り」(error of the first kind)といいます。
一方で、真実は1,500万円以上の平均年収で、仮説が「1,500万円以下である」というものだった場合、本来はこの仮説が棄却されないといけないのに棄却されなかった場合、これを「第二種の誤り」(error of the second kind)といいます。
第一種の誤りも第二種の誤りにも優劣というのはありませんが、仮説によってはより避けるべき誤りというのは出てきます。例えば、会計士の財務諸表監査を考えてみましょう。この場合、「財務諸表は適正である」という命題を検定します。真実は「財務諸表が適正」だとします。この場合、「適正ではない」という結論を出すのが第一種の誤りです。次に、真実は「財務諸表は適正ではない」だとします。この場合、「適正である」という意見を出すのが第二種の誤りです。ここで第一種と第二種の誤りを検証してみましょう。
第一種の誤りの場合は、「適正ではない」という結論に監査人が達したとしても、現実では追加の監査手続きなどが行われ、最終的には「適正だった」という結論に変化していきます。このため、第一種の誤りというのは、追加の監査手続きなどのコストが発生するだけであり、最終判断に至る間で誤りが修正される可能性が高いものといえます。
一方で第二種の誤りは、「適正である」という判断をしてしまったために追加の監査手続が行われることもなく、そのまま「適正である」という結論となってしまう可能性が非常に高いものと考えられます。
このように比較すると、「財務諸表は適正である」という命題で考えた場合、第二種の誤りの方が社会的なコストは多大になってしまう可能性があり、第一種よりも第二種の誤りの方に重きをおくべきだと考えられるのです。
現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。

