現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。
(平成23年7月1日現在)
はじめに- バリュエーションにおける確率・統計学
近年、自然科学の分野だけでなく、人文科学の分野においても確率統計学的検討が行われています。このバリュエーションの分野においても、確率・統計の概念は非常に重要なファクターを占めており、バリュエーションを理解する上では不可欠なものといえます。しかし、確率・統計の概念は、非常に高度な数学が用いられることから学問的に理解するのは非常に難しい分野であり、これがバリュエーションの十分な理解の妨げとなっていると言っても過言ではありません。
このバリュエーションシリーズ補論では、「実務的な」視点でバリュエーションのナレッジ情報を提供することを目的としていることから、確率・統計の数学的な精緻さを求めず、確率・統計の直感的な理解に努めることを目指しています。また、あくまでも、ファイナンスのバリュエーションの世界で利用される確率・統計の概念にのみスポットをあて、ベイズ確率といったものについては特に解説しません。
1-1.度数分布とヒストグラム
確率・統計を理解するために、まずは1つのデータを利用して、統計の概念を把握していきます。
例えば、大学で数学の試験を実施したところ、次のような結果となったとします。
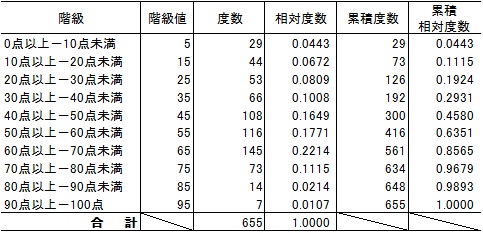
上記のような表のことを、度数分布表といいます。度数分布表では、階級(class)に分けて、階層ごとの度数(frequency)を集計しています。この場合の度数は、人数になります。階層値は、その階層の代表値で一般的にその階層の平均値をとります。
階層は今回は10点刻みの10階層で行いましたが、階層の幅と階層数の決定に必ずしも決まりがあるわけではありません。一般的には、スタージェスの公式というものがあり、これによって決定することが多いように思われます。
【スタージェスの公式】
階層数をkとすると、次のように階層数を求められる。
![]()
相対度数(relative frequency)は、全体のうち、その階層がどの程度の割合を占めているかを把握するものです。また、累積度数(cumulative frequency)は第1階層から順次度数を足し上げていったもので、累積相対度数(cumulative relative frequency)は、相対度数を第1階層から足し上げたものになります。今回の数学のテスト結果では、45.8%の生徒が50点未満であったことが累積相対度数で理解することができます。
この度数分布表をグラフ化したのが、ヒストグラム(histogram)です。
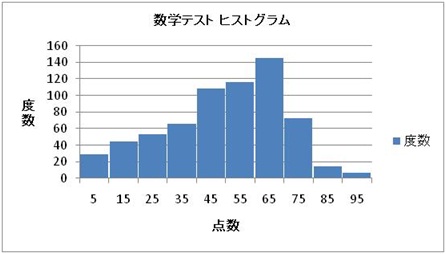
ヒストグラムは視覚的に度数分布の結果を把握することができるものです。このヒストグラムも70点以上の学生はぐっと減り、非常に難しいテストだったことが見た目で理解できます。
1-2.分布の形状と代表値
度数分布(ないしヒストグラム)の形状がどのようになっているか決定する尺度が、代表値(average)と散らばり(dispersion)です。本項では代表値について解説し、次項で散らばりについて解説します。
代表値は、その母集団を代表するような値のことで、平均(mean)、メディアン(median)、モード(mode)の3つがよく利用されています。
(A) 平均
平均は、一般的にもよく利用されている代表値ではないかと思います。平均も算術平均(arithmetic mean)、幾何平均(geometric mean)、調和平均(harmonic mean)がありますが、それぞれの平均にはそれぞれの目的があるため、その目的に合わせて利用します。ファイナンスでは算術平均と幾何平均がよく利用されます。
【算術平均】
![]()
【幾何平均】
![]()
平均は、分布のちょうど重心となります。
(B) メディアン
メディアンは、中央値・中位数と呼ばれることもあります。メディアンは、データを小さい値から順番に並べ替えて、その中央にくる値のことです。平均値の場合は、極端に高い値や低い値があるとそれに影響されて値が変わるものの、メディアンはデータ個数のちょうど真ん中に位置するものであるため、極端に高い値や低い値のものに影響を受けません。
(C) モード
モードは、最頻値です。つまり、ヒストグラムの中で最も発生する値の部分で「峰」の部分になります。
(D) 平均、メディアン、モードの関係
上記の平均、メディアン、モードは、左右対称の分布であれば、すべて一致します。しかし、左右のどちらかに歪んでいると、平均、メディアン、モードは一致しません。このため、分布の形状を把握する場合、その歪み具合を把握するのに、代表値によって把握することができます。
1-3.分布の形状の散らばり
分布の形状を特徴づけるのは、代表値と合わせて、散らばりが重要な要素となります。
散らばり具合を表す概念として、偏差(diviation)というものが利用されます。偏差とは、ある基準から、観測値がどれぐらい離れているのかを表したものです。例えば、平均偏差(mean diviation)と呼ばれるものがあり、これは各観測値が平均からどれぐらい離れているかの平均を求めるもので次のようになります。
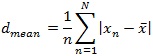
しかし、この平均偏差は上記のように絶対値計算が必要(符号をなくす)なため、数学的に取扱いが煩雑になります。そこで、偏差を2乗することで符号をなくし数学的な取扱いを楽にした散らばり具合を表現しようとしたのが、分散(variance)です。
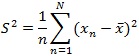
そして、分散の平方根をとったものが、標準偏差(standard diviation)です。
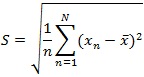
数学的な扱いやすさからファイナンスでは平均偏差ではなく標準偏差を利用することがほとんどです。
1-4.分布の標準化
分布におけるデータは、1次変換することができます。1次変換とは、位置および尺度について変換するものです。一般的に次のように表せます。
![]()
この1次変換によって、平均、分散、標準偏差は次のように変換されます。
![]()
データの1次変換でよく利用されるのが、標準化(standardization)と呼ばれる変換です。標準化は、平均0、標準偏差1となる1次変換です。標準化の1次変換は、次のaとbを1次変換式に代入すれば確かめられます。
![]()
異なる分布のものを標準化することで、同等に扱うことができます。ファイナンスでは標準化された分布(標準正規分布など)を用いられることが多いです。
現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。

