現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。
(平成23年11月30日現在)
4-2-3.DCF法における割引率の算定
DCF法の算定において、その設定における判断が最も難しいのが割引率の妥当性です。4-2-1、4-2-2で算定された予測期間の将来キャッシュ・フローと継続価値TVを現在価値ベースに割り引くための割引率にどのように求めるべきなのか、現在でも様々な研究・議論が行われています。
本項では、DCF法において最も利用されているCAPMによって算定された株主資本コストを利用した、加重平均資本コスト(WACC)の利用を前提に解説します。
(1) 加重平均資本コスト(WACC:Weighted Average Cost of Capital)の基本的な考え方
DCF法においては、負債コストと株主資本コストを加重平均した加重平均資本コスト(WACC)が一般的に利用されています。加重平均資本コストは、評価対象企業の調達コストを「他人資本(負債)による調達コスト」と「自己資本(資本)による調達コスト」のそれぞれで算定し、調達源泉割合に応じて加重平均することで資本コストを算定する方法です。
WACCの利用は、調達源泉の状況を企業価値評価に織り込むのに最もわかりやすい方法と言えます。また、DCF法では評価実施時点でのWACCを算定し、その後WACCが一定であるという仮定のもとで計算します。この点、LBO等により負債調達割合が高い状況で企業価値を評価した場合、負債コストが極端に高い割引率が算出され、徐々に(もしくは資本政策により急激に)負債比率が下がることが想定されているLBOの状況をWACCに反映できないというデメリットが存在します。ただ、そもそもWACCの算定自体に様々な仮定が用いられ、高度な判断、裏返せば、主観的判断が入る余地が多分にあるため、これをさらに主観的な判断において変化させる(予想する)となると、妥当性の検証が難しくなるきらいがあるため、WACCを一定として用いることにも一定の合理性はあります。
なお、上記のLBO等の極端なケースでは、割引率を一定としない評価モデルを採用するケースも考えられます(※「APV法」にて後述)。
(2) 負債コストの算定
WACCの計算には、負債コストと株主資本コストのそれぞれを算定し、資本構成割合に応じて割引率を算定することになります。
負債コストは、負債(借入金や社債等)による調達コストを算出します。負債コストは、有利子負債の金利部分であるため、「有利子負債コスト」と呼ぶケースもあります。実務的には、支払利息(借入利息や支払利息、割引料など)を利用することで算定するのが一般的です。支払利息は、その企業の信用リスクを織り込んだ形で貸出利息が決定されているという仮定のもとで適切な負債調達コストを示していると考えられているからです。
日本の場合、長年のメインバンク制や、日銀による超低金利政策(ゼロ金利政策)の長期化により、支払利息が適切な負債調達コストを反映していないのではないかという議論もあります。特に中小企業の場合は、担保価値や担保余力、保証人枠の信用度合等に借入利率が大いに影響を受けてしまい、適切な負債コストを示さない可能性もあります。しかし、こういった国政的な理由や担保等の理由も含めて、事実としてその利息で調達できていることが企業の信用力そのものであるし、将来的な負債コストを統計的に推定することは非常に困難であることから、支払利息をそのまま利用するのが妥当であると考えられます。
(3) 株主資本コストの算定
会社にとっての株主資本コストは裏返せば株主にとっての期待収益率と言えます。このため、株主資本コストの算定方法は、一般的に株式期待収益率を推定するCAPM(Capital Asset Pricing Model)という理論が用いられて行われます。CAPMによる株式期待収益率の算定式は以下のとおりです。
【CAPMによる株式期待収益率】
株式期待収益率= リスクフリーレート+β×リスク・プレミアム
①リスクフリーレート(risk free rate)
リスクフリーレートは、リスクのない(もしくは少ない)金融商品の期待収益率であり、実務的には国債利回りを用いるのが一般的です(もちろん国債にもデフォルトリスクがあり、完全なリスクフリーとは言えません)。「国債」といっても、数年の短期国債や10年の長期国債、20年・30年といった超長期国債などがありますが、実務的には10年物の国債利回りを採用するのが一般的です。理論的には、その株式の投資機関に相応した期間物を利用するのが最も妥当であると考えられますが、株式投資の場合、当該株式の投資期間を最初から決定することはできないため、概ね10年が利用されているように思われます。短期国債ではインフレリスクを織り込めていないし、30年の超長期になると実際にそこまで当該株式を投資し続けるという仮定に無理があるため、10年物が利用されやすいと考えられます。
②β(ベータ)
次に、β(ベータ)とは、株式市場全体の株式利回りと個別企業の株式利回りの相関関係を示した指標です。これは、システマティックリスクのリスク量を表す尺度です。ここで、システマティックリスクとは、次のようなものです。
| 内 容 |
|
システマティックリスク(Systematic Risk) 資本市場全体に存在するリスクであり、分散投資をしても排除できない(すなわち、どのような投資ポートフォリオを構築しても排除できない)リスクのこと。 |
|
アンシステマティックリスク(Un-Systematic Risk) 資本市場全体に存在するリスクではなく、投資対象企業固有の何らかのリスクのこと。 |
システマティックリスクとは、分散投資理論によってもなお排除しきれないリスクのことであり、株式投資をしている以上は全投資家が負うリスクのことです。一方で、アンシステマティックリスクは、個別企業固有のリスクであり、分散投資理論を用いれば回避できるリスクです。
CAPM理論は、資本市場において投資家が負うリスクプレミアムはシステマティック・リスクのみであり、株主資本コストはシステマティックリスクによって算定することができるというものです。アンシステマティックリスクについては経済合理的な投資家であれば分散投資によってリスク回避しているので、CAPMではアンシステマティックリスクについては一切考慮しないで期待収益率を求めることになります。
このシステマティックリスクと個別株式のリスクとの相対的尺度がβ(ベータ)になります。例えば、β=1の場合、当該個別企業の変動性は株式全体の変動と全く同一の動きをしていたことを示します。また、β=1.5の場合、株式市場全体の株価が1%上昇したときに、当該個別企業の株価は1.5%上昇したことを示します。つまり、βが1より大きい場合には株式市場に比べて当該個別企業のリスクは高いといえ、βが1より小さい場合には株式市場に比べて当該個別企業のリスクは低いと言えるのです。なお、この場合の「株式市場全体」はTOPIXをインデックスとするのが一般的です。
βは、株式市場全体の利回りの動きと個別企業の投資利回りの動きの相関関係を示すリスクの尺度です。投資市場におけるリスク指標は、「分散」ないし「標準偏差」を用いて行われますので、βの算定でも分散を用いて算定されます。具体的には、個別企業の投資利回りと株式市場全体の投資利回りの共分散を求め、この共分散を株式市場全体の投資利回りの分散で除して求めることになります。
なお、非上場企業におけるβ(ベータ)については、次項により解説します。
③リスクプレミアム(risk premium) と小規模アンシステマティックリスク
リスクプレミアムとは、株式投資によって求める株式投資家の見返り部分で、株式利回りとリスクフリーレートの差額となります。株式投資というリスクを伴う投資行動をする以上、投資家がリスクフリーレートの金融商品に投資していればリスクなしで得られたであろう利回り以上の超過利回り部分を見返りとして求めるのは当然であり、それがリスクプレミアムとなります。
リスクプレミアムの算出は株式市場全体の過去株価データ等の大量のデータ処理が必要になるため、通常は情報ベンダー企業(イボットソンジャパン)などから入手します。
なお、CAPMの一部修正として、リスクプレミアムにおいて企業規模に関するアンシステマティックリスクを考慮する可能性があります。一般的に、小規模事業会社の株式は大企業の株式よりもリスクが高く、高い投資利回りが要求されるのが基礎研究などで明らかになっています。イボットソンといった情報ベンダーでも、規模に応じたリスクプレミアムを公表しており、評価実務においても規模を考慮したリスクプレミアムを用いて評価が行われます。
④小規模アンシステマティックリスク以外のリスクについて
企業規模等のアンシステマティックリスクについては、CAPMを前提としている以上、割引率の算定では考慮しないのが一般的です。アンシステマティックリスクについては、割引率に考慮せず、どちらかというと評価結果を受けて最終的に取引価格を決定する際に考慮することになります。アンシステマティックリスクを割引率計算に加味するとすれば、どのようにしてアンシステマティックリスクを定量化したのか、そのモデルに対する十分な判断と理解が必要となるのではないかと思われますので一般的に行われません。
(5) WACCの算出
上記の方法により算定された負債コストと株主資本コストを用いて、加重平均資本コストWACCを求めます。
WACC=(負債×負債コスト+純資産×株主資本コスト)/(負債+純資産)
なお、負債および純資産は簿価ベースではなく時価ベースを用います。このため、純資産は株式時価総額になります。負債も本来は時価評価されたものとなりますが、実務的には評価コストとの兼ね合いにより簿価を用いることも多いと思われます。
4-2-4.DCF法における非上場企業のβの算定
上項のとおり、βは上場企業の公開株価を用いて計算されるもので、非上場企業の場合、直接βを計算することができません。その結果、株主資本コストが計算できず、WACCが計算できなくなってしまいます。
このため、非上場企業の場合、公表株価が存在しないため直接βを求めることができず、類似公開企業のβを利用することになります。しかし、当該βは類似企業の財務構成を反映したものであるため、評価対象企業のβとしてそのまま利用すると理論的な整合性が取れなくなります。なお、資本構成を反映したβをレバードベータ(Levered Beta)といいます。非公開企業のβを求める場合には、類似企業のレバードベータから、資本構成を除外したアンレバードベータ(資産ベータ)を算出し、そこから評価対象企業の資本構成を反映したレバードベータへの変換(リレバー)を行うことになります。
①資産ベータ(アンレバードベータの算出)
まず、資産ベータ(アンレバードベータ:Unlevered Beta)と呼ばれる負債の存在しない状態のβを求めます。資産ベータは、次の式により求めます。
【資産ベータの算出】
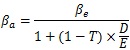
類似企業の選定は、マーケット・アプローチのときと同様に、数社もしくは十数社を類似企業として選定し、それぞれのレバードベータ(いわゆる通常のβ)を算出します。そこから、上記の算式に当てはめて各社の資産ベータを算出し、平均的な資産ベータを求めることになります。
②リレバー(評価対象企業のレバードベータの算定)
次に、上記の資産ベータから、評価対象企業の財務構成を反映した形で、レバードベータを算出(リレバー)することになります。
【リレバーの算出】
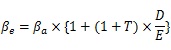
①で算定された資産ベータを評価対象企業の財務構成に基づいて、リレバーしレバードベータを求めます。
4-2-5.DCF法における事業価値から株主価値の算定
上記のように、分子となるキャッシュ・フロー、分母となるWACCを算定したら、以下の式で事業価値を算定します。
【DCF法の事業価値計算】
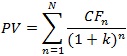
| PV | :現在価値 |
| N | :将来キャッシュフローの予想される最終年度 |
| CFn | :n年度の予想将来キャッシュフロー |
| k | :割引率(WACC) |
また、継続価値TVを分離した場合は以下のとおりとなります。
【継続価値を分離したパターン】
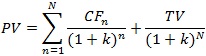
上記のとおり、事業価値が算定できたら、下記のとおり、株主価値を計算します。
【株主価値の計算式】
株主価値= 事業価値 + 非事業価値 - 有利子負債
現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。

