現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。
(平成23年7月1日現在)
2-1.相関とは
前項までは、1つのデータから得られる分布の状況を示す指標(代表値や散らばり具合)について解説しました。
本項では、2つ以上のデータを取り扱う場合についての、相関(correlation)と回帰(regression)の概念について解説します。数学的な単純化を図るため、変数は2変数として解説していきます。多変数の場合は多変量解析のための数学的技術が必要となり、バリュエーション実務のレベルを超えるため解説しません。
相関とは、2変数をそれぞれ独立したものとして取り扱い、その結果、2つの変数に何らかの関係があるかを考えるものです。2つの変数の関係を相関関係といいます。一般的には、2つの変数をプロットした散布図(scattergram)において直線的な関係があるものを「相関関係がある」といいます。また、1つの変数が増加するにつれて、もう一方の変数も増加する場合には「正の相関関係がある」といい、逆の関係の場合に「負の相関関係がある」といいます。また、この直線具合によって、「強い正の相関会計がある」という場合もあります。強い正の相関の散布図は、次のようなものです。
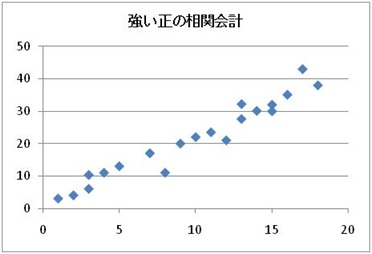
上記の散布図は、ほぼ直線上に2つの変数がプロットされており、右上がりであることを目視でも確認できるぐらいであり、強い正の相関関係があるといえます。
2-2.相関係数
上項では散布図において「見た目」から相関関係をとらえました。
しかし、(当然ではありますが、)定量的な表現として相関関係を図る必要があります。それを扱うのが相関係数(correlation coefficient)です。相関係数には様々なものがありますが、相関係数としては積率相関係数(product moment correlation coefficient)を一般的に利用します。本シリーズでも積率相関係数を相関係数として取扱います。
積率相関係数は、次のように定義することができます。
![]()
上記の式における最初の式の分母はxとyの標準偏差となります。分子のxとyの偏差の積の平均は、共分散(covariance)といいます。つまり、積率相関係数は、2変数の共分散をそれぞれの標準偏差で割った値となります。
相関係数の最大の特徴は、ー1から1の範囲となることです。特に、-1の値をとるとき「負の完全相関」といい、1のとき「正の完全相関」といいます。
2-3.回帰分析とは
2つ以上の変数の取扱いにおいて、重要な概念として相関と同様に理解しなければならないのが、回帰の概念です。回帰は、ある変数がもう一方の変数の決定に何らかの影響を与えているのではないかという見方で2つの変数をとらえようとするものです。
2つの変数x、yを考えた場合、xがyの決定に何らかの影響を与える関係にある場合、xを独立変数(independent variable)ないし説明変数、yを従属変数(dependent variable)ないし被説明変数といいます。そして、この2つの変数の関係性を探るのが回帰分析(regression analysis)になります。
回帰分析には様々な方法があり、ファイナンスでも様々な方法が利用されています。ここでは、回帰分析の基本的なものとして、最小二乗法による1元1次回帰分析(1つの変数を用いた直線的な回帰分析)について解説します。
1元1次回帰分析は、次のような1次式でxとyを表現することになります。
![]()
すなわち、回帰分析は、上記1次式の係数であるaとbを求めることに他なりません。
ここで、この1次式を求める方法として一般的に利用されるのが最小二乗法(method of least squares)です。最小二乗法とは、あるxから推察されるyの値と、実際の観測値との差額の和が最も小さくなる直線(1次関数)を探し出す方法になります。実際には、数学的な取扱いを簡素化するため、符号を取り除くため差額の二乗の和を使います(このため、「二乗法」と呼ばれている)。最小二乗法は次のように表現できます。
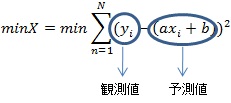
上記の式は、2次式であるため、a、bをそれぞれ偏微分してゼロとなるa、bのときに最小となります。次の連立方程式が成立します。
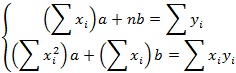
この連立方程式を解くと、次のようになります。
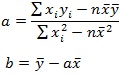
これをもとの1次式に代入して求められたのが回帰直線(regression line)です。
なお、上記の回帰分析では、1元1次の回帰について解説しましたが、説明変数を2つ以上にした重回帰(maltipke regression)や1次ではなく2次式や3次式の回帰を行う多項式回帰(polynominal regression)なども考えられます。重回帰では、例えば2つの説明変数を利用すると3次元における平面的な当てはめを求めることになります。ファイナンスでは例えば時系列、株価、ボラティリティといった3つの関係を表現するのに重回帰が行われたりします。また、多項式回帰では、イールドカーブの生成等でも理解できるように、ファイナンスにおいて曲線で表現されるものも多いため、3次式などの回帰分析はしばしば利用されています。
現在、こちらのアーカイブ情報は過去の情報となっております。取扱いにはくれぐれもご注意ください。

